[TWDS 線上版聚] 因果推論在行銷上的應用

[2021/10/30] Taiwan Data Science Meetup — 黃大維 David Huang

講者介紹

David 目前在哈佛商學院 (Harvard Business School) 攻讀量化行銷博士，研究專注於客戶生命週期管理，利用因果推論、機器學習等方法解析早期使用者的行為，並幫助企業設計個人化體驗與精準行銷模型。

過去 David 所累積的實務經驗也非常豐富，包含曾任職 Migo.tv (熱鬧點科技) 資料科學團隊主管、Applied Predictive Technlogies（現萬事達卡資料顧問部門）顧問、英睿科技資料科學家等。工作中協助東南亞與大中華區的指標企業導入資料科學架構，解決使用者體驗優化、個人化演算法設計、客戶偏好分析、新產品導入與訂價、客戶長期價值管理等重要商業問題。

分享主題

資料科學的進展讓行銷領域在過去十年內有重大的變化 — 利用自然語言理解消費者評論並找出潛在需求、透過推薦系統打造個人化體驗、運用機器學習方法預測高流失風險客戶並設計留存策略。然而，根據消費者真的會因為評論中提到的產品功能而購買產品嗎？個人化演算法真的有讓消費者有更好的體驗嗎？客戶真的有因為留存活動繼續使用產品嗎？這些問題的核心都是「因果推論」，但真實世界複雜多變，要真正能找出「策略」與「價值」間的因果關係並不容易。此次 David 將分享因果推論中的辨識 (Identification) 問題與策略，並分享他們在行銷領域的應用。

內容大綱

1. 為什麼需要因果推論 — 「預測已不能解決企業面臨的所有問題」

2. 辨識問題的因果關係

3. 在自然實驗中辨識因果關係的方式

4. RCT實驗中運用的新技術

5. Q&A

6. 為什麼需要因果推論 — 「預測已不能解決企業面臨的所有問題」

針對業界實際面臨的問題，David舉出了兩個案例：

電信公司推出簽約優惠是否能降低顧客流失率

實務上可以分為兩種可行的做法：

1. **運用機器學習模型做二元分類，預測最有可能流失的客群
   ** 根據過去的資訊(例如：通話時數、瀏覽網站)，來建立顧客流失模型，以預測個別用戶的流失機率，針對流失機率高的用戶發送簽約優惠。
   結果：流失機率高的用戶族群，對活動的反應不一定比較好(下圖RISK)。
2. **執行隨機控制實驗(RCT)，預測推出活動對於各個客群的具體影響
   ** 先做 A/B 測試搜集資料，接著建立增益模型 (Uplift Models) 預測「 特定用戶如果有收到活動，流失機率下降了多少？ 」
   結果：預測流失機率下降最多的客群，對活動的反應最好(下圖LIFT)。

資料來源 | Ascarza, E. (2018). Retention futility: Targeting high-risk customers might be ineffective. Journal of Marketing Research, 55(1), 80–98.

從傳統機器學習的預測模型中，我們無從得知顧客參與活動後，有哪些行為上的改變，因此需要透過實驗了解商業決策具體的因果關係。

快銷品公司想知道如何訂定乾洗手的價格折扣

同樣有兩種做法：

1. 以機器學習模型預測價格與數量的關係
   使用 傳統機器學習模型 (如regression model, boosting tree等)，或運用 cross-validation 預測不同價格下的銷量，缺點是忽略市場條件是不斷變動的，因此結果容易失準。
2. 納入市場的供給需求因素，衡量價格與數量之間的關係
   疫情爆發之初，消費者需求強勁帶動了價格上升，一段時間後，隨著供給數量增加，價格也落回到原本的水準。

若忽略市場的供給需求影響，只以原始的價量關係思考策略，很可能會出現偏誤，將市場這項干擾因子(Confounder)納入考量後，才能在未來市場情境變化時，預測出需求數量的變動，因此經濟學中採用「 結構因果模型 」 (Structural Causal Model) 進行估計，雖然配適資料上可能不如機器學習模型，卻能更好的預測市場環境變化下價格與銷量的關係 (Counterfactual Analysis)。

接著，David也提到幾個常見的實驗及研究方式：

資料來源 | Bojinov, I., Chen, A., & Liu, M. (2020). The importance of being causal. Harvard Data Science Review.

1. 隨機控制實驗(RCT)
   優點是 實驗與對照組可以完全比較 (SUTVA)，以電信公司的例子來說，參與活動者(實驗組)與未參與者(對照組)，能在相同的基礎下互相比較。
   然而，此研究方法也面臨 社群網絡效應的挑戰 ，以臉書動態為例，當我們看到特定動態內容，通常會分享或是與發文者互動，此時將連帶影響周圍的人會看到的文章、決策的方式，使周遭的朋友也連帶成為實驗的一環。
2. 自然實驗(Natural experiment)
   只在特定假設、情境下發生，需要依照個案情況驗證合理性，而處置變數 (treatment variable) 存在自然的變異情況。
3. 相關性研究(Correlational study)
   雖然相關性並不等於存在因果關係，但是此研究方法對於假說的產生很有幫助。

2. 辨識問題的因果關係

透過繪製有向循環圖(DAGs)，能夠更了解變數之間的關係。

• 以電信公司的例子來說，電信公司想透過用戶過去的通話習慣、原始費率等資訊(X)，知道下期發給他折價券(W處置)，是否會降低其流失率(Y)，在此例子中，W與X之間不存在因果關係，因此容易辨別W對Y的因果關係。
• 以快銷品公司的例子來說，需求與供給面的變量(X)會影響銷量(Y)，欲知道價格的變化(W)對銷量的影響，但是X、W之間會互相影響，且都會導致Y的變化，此時若想要單純看價格變化(W)對於銷量的影響，就需要考慮找其他的變數進來。

若想要實作DAG，找出因果關係辨識條件 (identification condition) 可使用： R語言dagitty套件、Python的 CasualDAG 套件。

辨識因果關係的常見問題

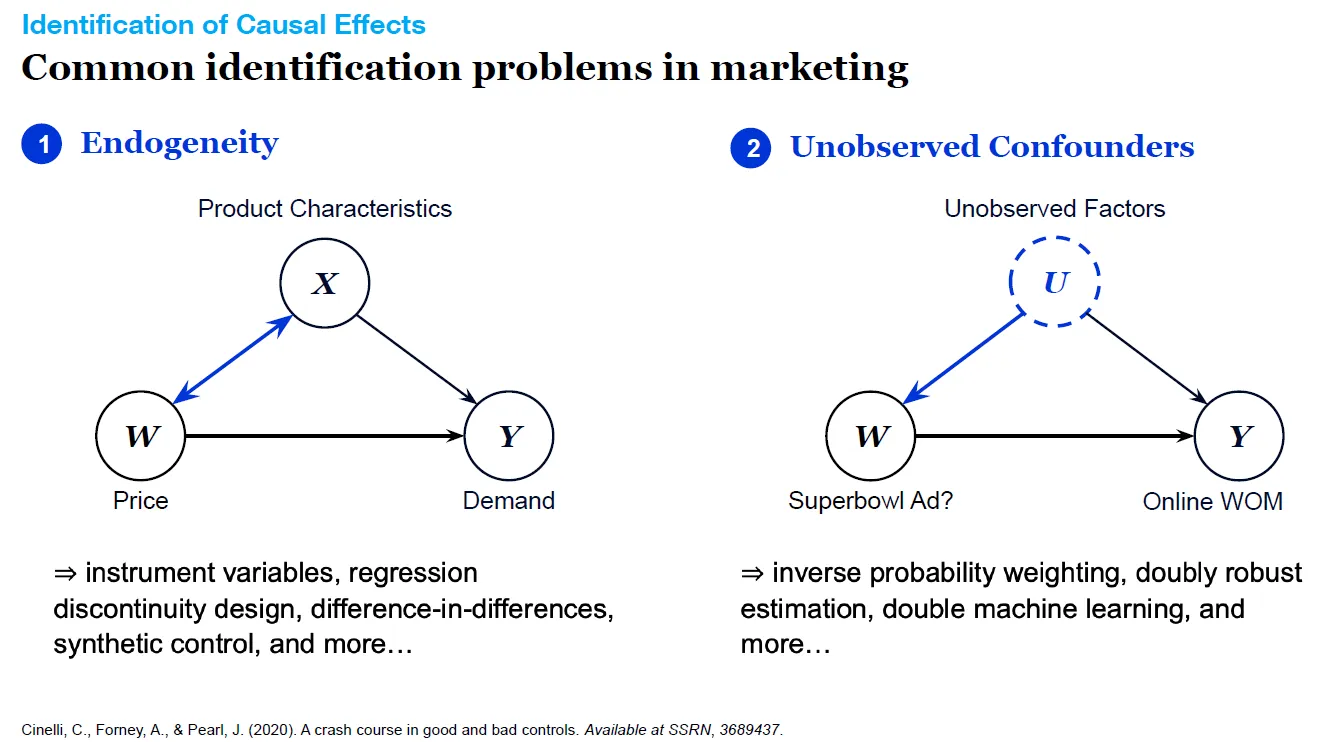
1. 內生性問題(Endogeneity) ：變數之間相互影響，使模型估計產生偏差。
2. 未觀察到的的干擾因子(Unobserved Confounders) ：存在共同影響W與Y的因素未被納入討論。
   例如，企業想要瞭解購買超級盃廣告後口碑行銷的效益如何？可能需要思考其他變因，像是企業品牌形象與超級盃的契合度、代言人本身形象等。

常見的兩種選擇性偏誤

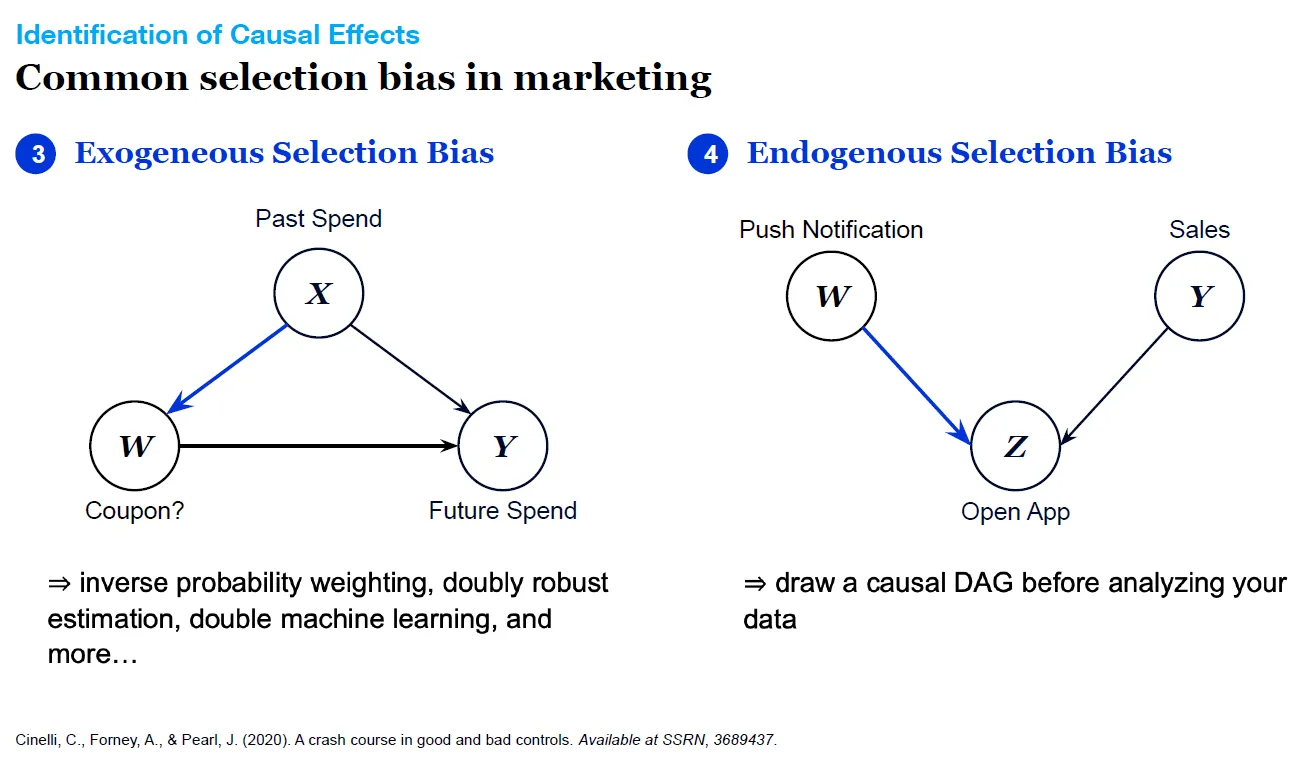
1. 外生選擇性偏誤(Exogeneous Selection Bias)

• 以電商平台為例，平台通常通常根據過去消費習慣，決定是否發放折價券給使用者，因此需要衡量發折價券優惠是否會增加顧客未來的消費。
• 事實上過去消費多寡經常影響著未來的消費量，而企業進行分析時往往會誤以為折價券優惠才是推升顧客消費的主因。

2. 內生選擇性偏誤(Endogenous Selection Bias)

這裡提供兩個常見的例子：

1. 運用手機推播購物訊息是否會帶動銷量成長？

針對「有點開 App 的人」分析推播對購買機率的影響，發現有點擊推播的人購買機率反而較低。然而，主要原因是推播讓很多沒有購買意願的人不小心點開了 App，而不是推播造成了反效果。

2. 患有糖尿病的患者比較容易確診COVID？

做PCR檢測者本來就屬於健康狀況不佳的族群(如糖尿病患者)，因為經常出入醫療院所，容易受到檢測，而做了檢測才會確診出COVID，忽略其中的原因時，就容易做出錯誤的結論。

可參考這篇論文：Collider bias undermines our understanding of COVID-19 disease risk and severity

3. 在自然實驗中辨識因果關係的方式

斷點迴歸分析：Uber 的加成訂價 (surge pricing) 對需求的影響

關鍵問題 ：同一地點當有很多人都想叫車時，Uber會以1.25為分界點，給予較平日高1.2或1.3倍之收費(稱為surge pricing)，欲知該定價方式對於消費者的購買率有何影響？

使用方法 ：斷點迴歸法 (Regression Discontinuity Design)

資料來源 | Cohen, P., Hahn, R., Hall, J., Levitt, S., & Metcalfe, R. (2016). Using big data to estimate consumer surplus: The case of uber(No.w22627). National Bureau of Economic Research.

觀察在1.25 倍附近的購買率，估計價格成長 10% (1.2→1.3) 對顧客搭乘意願的影響。

此處只有估計出市場條件在 1.25 倍情況下漲價 10% 的影響，不一定跟在 2.05 倍的市場條件下漲價 10% 的影響相同。因此，我們只估計出 local average treatment effect(2021年諾貝爾經濟學獎得主的重要貢獻)。

合成對照組： 速食店裝設自助點餐機對銷量的影響

關鍵問題 ：在速食店內提供自助點餐機是否會影響銷售量？

存在外生的選擇性偏誤 ：自助點餐機之有無(W)、店家特性(X)皆會影響銷售量(Y)，然而店家特性(X)也影響自動點餐機之有無(W)。

右方圖表中藍色線代表使用點餐機之店舖的月銷售狀況，灰色線則是其他店舖的銷售金額，虛線代表實驗店舖裝設自助點餐機的時間點。

因為裝點餐機的店舖跟沒有裝設的店舖無法互相比較，使用「 合成對照組 」方法，利用沒有裝設的店舖的銷量進行加權平均（利用 OLS regression 或其他機器學習方法），預測實驗店舖「如果沒有裝設自助點餐機」的表現。

結果顯示：使用自動點餐機的店鋪之銷售情況，與合成對照組之預估月銷售量相比明顯較佳。

延伸：矩陣補全方法 (Matrix Completion Method)

當不同店鋪在不同時間點推出活動 / 不同市場不同時間點推出廣告，不容易編制出合成對照組，此時可以利用機器學習中的 Matrix Completion Method 造出「合成對照指數」。

4. RCT實驗中運用的新技術

1. 增益模型(Uplift model)
   常用於廣告推廣的最佳化，例如：觀察隨機實驗中收到優惠券的顧客，與對照組顧客之購買行為差異，並預估未來的成效。常用套件如：CausalML, EconML等。
2. 因果樹(Causal Tree) 與因果森林 (Causal Forest)

• 不同於一般決策樹是以最大化不純度指標 (Impurity Measure)做分枝，因果樹是以最大化「 實驗組與對照組的平均落差 」為分枝條件。
• 為了避免 ovefitting，以 honest estimation 方法進行分枝：將樣本分成兩組，一組用來分枝，另一組用來估計各個節點「實驗組與對照組的平均落差」。

3. Surrogate Index Approach

以短期指標(S)來了解實驗(W)對於長期表現(Y)的影響。

5. Q&A 精選

Q1：因果關係的分析成本相對高，業界做決策時真的在乎這些分析嗎？

• 很多大公司會將實驗設計與分析的結果，作為實際決策時的參考，但是亞洲企業不一定會花時間、成本做因果分析，美國的大型電商或是社群平台都會很在意這塊，而現在要進行因果推論都有現成的工具能使用，只要了解這個模型與使用情境，實際操作已不是那麼困難，不妨可以嘗試接觸。

Q2：針對Unobserved confounder這項問題，通常的情況是you don’t know what you don’t know，請問有哪些解決方法？

• 必須依靠domain knowledge，例如今天想了解推薦系統對於消費者收看影集的影響，但事實上除平台的的推薦系統外，社群上的討論也經常是影響消費者是否觀影的因素，因此在探索性資料分析中，擁有領域知識比較容易找到隱藏的變量，但這確實是一項難解的問題。
• 經濟學上的instrument variable 很常用來解決這個問題，也就是跟W有關但是跟confounders 無關的變數，能幫助我們捕捉W的變化，同時不會有內生性問題。

Q3：如何從多個推廣活動中選擇一檔活動執行，進行因果關係的推論？

• 透過過去的活動，可以找出哪些活動對於顧客相對有效(候選名單)，跑小型的樣本實驗(1000–2000筆)分析哪一檔活動的效果較佳，跑隨機測試看看結果哪個較好。

Q4：從簡報的DAG中entity節點數量都不多，但實務上分析時，面對的變因其實可能有成千上百個，這種情況會怎麼處理？目前想到兩個方式，一是把所有變因全部當成因果推論模型的輸入，讓套件自己找到之中的因果關係，二是先做一些假設和篩選自行排列組合，不知道正不正確？

• 建議先做一些假設，如果一開始就將所有的變量都塞進去，有可能會有問題，如果不確定變數是否有關係，建議可以使用貝氏網絡(Bayesian network)的方法，去觀察W與Y之間的因果關係，而降低維度不是一切問題的解答。

Q5：研究上Causal inference會以Graph neural network的方法來實做嗎？

• 我目前沒有特別探索這個領域。如果是想要用複雜的機器學習模型預測處置效果，可以參考 double machine learning 的論文。 但結合兩者可能是有趣的方法。

Q6：想請問本身是經濟系的，研究上很在意因果關係的效度，滿好奇所以在業界很多都是有相關性就直接採取行動了嗎？比如說電商平台發現某類過去消費行為的人很容易會購買某種商品，但其實可能是有某種confounding factor是主因，只是剛好發現這個相關性。

• 從我個人的觀察中發現有些資料科學團隊並不關注因果關係，將相關性直接對應到因果關係，但還是取決於團隊對於該假設有無足夠的信心。

Q7：前面提及以短期指標預測長期效果的概念，類似於backtest嗎？

• 根據歷史資料，就可以估計短期和長期的關係 (S與 Y的關係)，確實與backtest概念相近。

Q8：模型經過分析上線後，母體情況卻已有所不同，模型是否會失效？

• 設定指標定期確認模型的成效，若發現成效不如預期時，可能是因為 covariance shift 或concept shift(X、Y關係改變)。Transfer learning 也許可以解決這個問題。

參考資料

• Ascarza, E. (2018). Retention futility: Targeting high-risk customers might be ineffective. Journal of Marketing Research, 55(1), 80–98.
• Berry, S. T., & Haile, P. A. (2021). Foundations of Demand Estimation (No. w29305). National Bureau of Economic Research.
• Bojinov, I., Chen, A., & Liu, M. (2020). The importance of being causal. Harvard Data Science Review.
• Pearl, J., Glymour, M., & Jewell, N. P. (2016). Causal inference in statistics: A primer. John Wiley & Sons.
• Cinelli, C., Forney, A., & Pearl, J. (2020). A crash course in good and bad controls. Available at SSRN, 368943.
• Cohen, P., Hahn, R., Hall, J., Levitt, S., & Metcalfe, R. (2016). Using big data to estimate consumer surplus: The case of uber(No.w22627). National Bureau of Economic Research.
• Abadie, A., Diamond, A., & Hainmueller, J. (2010). Synthetic control methods for comparative case studies: Estimating the effect of California’s tobacco control program. Journal of the American statistical Association, 105(490), 493–505.
• Athey, S., Bayati, M., Doudchenko, N., Imbens, G., & Khosravi, K. (2021). Matrix completion methods for causal panel data models. Journal of the American Statistical Association, 1–15.
• Syrgkanis, V., Lewis, G., Oprescu, M., Hei, M., Battocchi, K., Dillon, E., … & Lee, J. Y. (2021, August). Causal Inference and Machine Learning in Practice with EconML and CausalML: Industrial Use Cases at Microsoft, TripAdvisor, Uber. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining (pp. 4072–4073).
• Wager, S., & Athey, S. (2018). Estimation and inference of heterogeneous treatment effects using random forests. Journal of the American Statistical Association, 113(523), 1228–1242.
• Athey, S., Chetty, R., Imbens, G. W., & Kang, H. (2019). The surrogate index: Combining short-term proxies to estimate long-term treatment effects more rapidly and precisely (No. w26463).
• Yang, J., Eckles, D., Dhillon, P., & Aral, S. (2020). Targeting for long-term outcomes. arXiv preprint arXiv:2010.15835.

筆手：邢芳瑜 (Ruby Hsing)
校稿：黃大維 (David Huang)
👉 歡迎加入台灣資料科學社群，有豐富的新知分享以及最新活動資訊喔！